Data Analysis and Manifold Learning (DAML) Lecture series by Radu HORAUD, INRIA Grenoble Rhone-Alpes Winter-Spring 2011 Short course description (pdf)

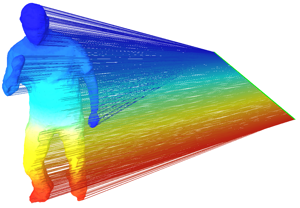
This is a 3D shape that is represented by an undirected weighted graph whose vertices correspond to 3D points and whose edges correspond to the local topology of the shape. Each graph vertex is projected onto the first non-null eigenvector of the graph's Laplacian matrix. This eigenvector may be viewed as the intrinsic principal direction of the shape, invariant to such shape deformations as articulated motion.

Lecture #1: Introduction to linear and non-linear dimensionality reduction.

Brief overview of spectral and graph-based methods, such as principal component analysis (PCA), multi dimensional scaling (MDS), ISOMAP, LLE, Laplacian embedding, etc.

Further readings: L. Saul et al. Spectral Methods for Dimensionality Reduction. O. Chapelle, B. Schoelkopf, and A. Zien (eds.), Semisupervised Learning, pages 293-308. MIT Press: Cambridge, MA.

Lecture #2: Properties of symmetric matrices.

Eigenvalues and eigenvectors. Practical computation for dense ans sparse matrices. Covariance matrix. Gram matrix.

Lecture #3: Graphs, graph matrices and spectral embeddings of graphs.

What is the matrix of a graph? Properties of graph matrices. Spectral graph theory. Undirected weighted graphs and Markov chains. Graph distances. Graph construction.

Lecture #4: The Gaussian distribution, Gaussian mixtures, and the EM algorithm.

The univariate and multivariate Gaussian distributions. The Gaussian mixture model. The expectaction-maximization algorithm for Gaussian mixtures. The curse of dimensionality.

Lecture #5: Principal component analysis.

Formal derivation. Linear discriminant analysis.

Lecture #6: Probabilistic PCA.

EM algorithm for PPCA. Bayesian PCA and model selection. Factor analysis.

Lecture #7: Laplacian embedding.

Spectral clustering. Semi-supervised spectral clustering. Links with other methods: Normalized cuts and random walks on graphs. Image and shape segmentation

Lecture #8: An introduction to kernel methods

Properties of kernels. Kernel PCA.

Lecture #9: Heat diffusion on graphs

Heat diffusion on Riemannian manifolds. Heat diffusion on graphs. Diffusion embedding. Scale-space representation. Choosing the dimension of the embedded space.

Lecture #10: Spectral graph matching.

Dense and sparse matching methods. Semi-supervised matching.

Lecture #11: Other manifold learning methods.

A list of (short) papers related to manifold learning:

• Robust Principal Component Analysis for Computer Vision
• K-means Clustering via Principal Component Analysis
• Charting a Manifold
• Learning High Dimensional Correspondences from Low Dimensional Manifolds

Lecture #12: Manifold learning applications

Medical image analysis, brain imagery, auditory perception, data mining, Google's PageRank algorithm, etc.